INTRODUCTION
All around us, we see different laws and different forces of nature at work. Riding a bicycle, cooking your favorite dish, boiling water to the emission of electrons or radiation of a black hole, everything is physics. While we often discuss how magnificent Einstein’s relativity theory is, or how elegantly we can get precise results from quantum mechanics, most of the time we tend to forget that everything around us is actually physics. These extremely important theories were developed when scientists were inspired by simple natural phenomena or were deeply conflicted when they couldn’t explain them with common intuition. Hence, it is essential to take a break now and then to find the essence of physics in daily life, infuse the feeling deep inside ourselves and start working again which is what I have done this past year.
I tried to convey to you why I took this break in the above paragraph but there’s also another reason(hopefully my writing’s not become rusty). These examples, all talk about Energy, which is responsible for(more examples) you vibing to your favorite music on your earphones or inhaling oxygen which provides energy to your entire body. Nope, I am not talking about a simple definition of ‘Work is Force times distance and Energy is the capacity to do Work and blah blah blah. NO! I am just telling you to marvel at the world around you, hold this feeling with you and never let it go. And if you must let it go, for whatever reason, then at least hold it for long enough so you can finish my article. Anyways, what I am gonna talk about today, is some properties of a system including energy. I still do not know how to do it but I really find Statistical Mechanics to be a beautiful subject and something which is not as popular as Quantum Physics or Astrophysics. Hopefully, my very limited readers will find it worth reading and share these articles with like-minded people if they find beauty in the subject as well.
SYSTEMS AND ITS PROPERTIES
You can fancy a lot of examples here like particles inside a box, a hot reservoir connected with a bath and etc etc etc. What I am gonna say is take your room as a system and think of it as an isolated one(the properties of your room are not affected by its surroundings and I know it’s not much of a realistic scenario but have faith in me on this one). When the system is isolated, we can think of its energy to be constant. Also, for the system to not interact with its surroundings, the walls of the system should be rigid, and impermeable so that the volume and no. of particles also remain constant. In this kind of system, the constant properties are energy, volume, and no. of particles. We shall denote Energy as E, Volume as V, and No. of particles as Np.
If you have studied gas laws, you must have heard of an equation that states
PV = nRT (1)
where P is the pressure, n is the no. of moles, R is the gas constant and T is the temperature.
The above equation is the equation of an ideal gas(What is it for a gas to be ideal? You can find it out yourself). The equation can be rewritten as
PV = NkT (2)
where nR = Nk. N is the no. of molecules and k is the Boltzmann constant. What I mean to say is that you have a system, and you know some of the properties such as E, V, and Np. The Energy of a system is generally written as
E = (3/2)kT (3)
So, we can find the Temperature(T) from here and(I’m not gonna explain how we are going to find out these properties but I’m gonna give you the feel and tell you that we can find out these properties) then the Pressure(P)(Keep in mind that equation(1) works only for ideal gases). In fact, if you know these macroscopic properties, you can find out other details about the system and one must ask the question, why must we shift to statistical mechanics?
THE NEED FOR STATISTICAL MECHANICS
If you look closely at the ideal gas equation, you see that we need the no. of moles(n) to calculate the equation. But we know that no. of molecules(N) is of the order of 1023 (If you know about Avogadro No. then you know). To find out about the evolution of a system, we must know its coordinates and momentum. By plotting these two together, we can find out how the system evolves. And there’s the catch! Unless you’re some sort of higher race of aliens with hyper-intelligence and have all your life to waste, you can’t calculate the properties of all the systems.
You can now come to realize that a system with so many molecules(N tends to infinity) is extremely complex and hence inherently tough and time-consuming with the above approach. What we’re gonna do now, is going to take the help of probability! It is important to emphasize that the system itself is not probabilistic as we can determine the evolution of the system if we have the information regarding all the identical subsystems within the system(i.e. all the gas molecules in an ideal gas).
To find out how the gas system evolves, let us assume that all the gas molecules behave the same way i.e. take the macroscopic properties of Energy, Volume, and No. of particles to be constant. Now, all the gas molecules are systems, and how each system acts, results in how the whole gas evolves. I know this is getting repetitive but I wanna make sure you understand this. For example, take an ocean as a system and treat every drop as a subsystem. You can get an intuitive feel this way. This group of subsystems defining how the whole system evolves is called an ensemble. An ensemble that has Energy, Volume, and No. of particles constant is called a microcanonical ensemble.
THE MECHANICS OF A SYSTEM WITH STATISTICS
First of all, we need two pretty damn simple definitions. The description of a system in terms of its macroscopic properties is called a macrostate while the description of a system in terms of its microscopic properties is called a microstate. Seems pretty basic right? Wanna go a bit deep? Let’s define another term!
The space where the coordinates and momentum of the ensemble are plotted(as we have already discussed that we need them to describe the evolution of the system) is called phase space. We have a function in physics called the Hamiltonian which describes the coordinates and momentum of a system and it can determine the energy of a system in simple words. Just so you might know. The surface plotted within the phase space due to the trajectories carved out by the system is called a hypersurface. This hypersurface must be bounded as the phase space determines the energy(just re-read this para if you didn’t get the hints) and of course, we don’t have something that can create energy out of nothing. The volume enclosed by the hypersurface is called hypervolume.
Now, if we get back to the macrostate thing. We can say that the energy of the system can be a macrostate. However, the system is an ensemble of subsystems and the constant energy E of the system is an arrangement of all the energies of the ensemble. All the possible arrangements of energies of the ensemble that make up the constant energy E are called microstates. Still a bit ambiguous? Let’s explore the difference with an example.
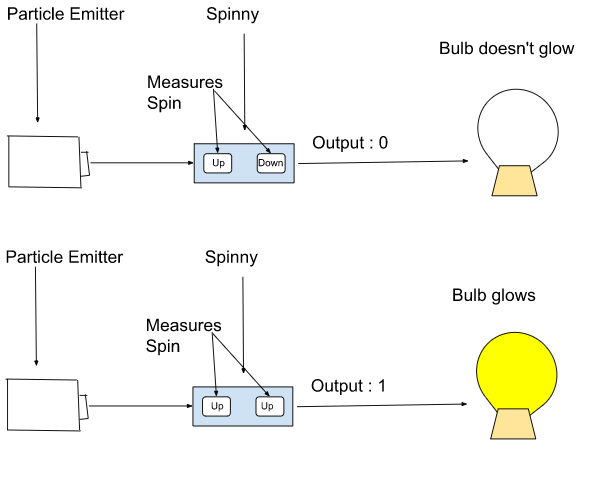
Similar to linear momentum and angular momentum, there is something called spin. Spin is a property of quantum particles. Let’s say a particle moves out of a box. A machine is placed at some distance from it. The box emits particles at the machine(let’s name our machine ‘Spinny’). Our Spinny measures the spin of the emitted particle. Let’s assume the box has two particles. They can either spin ‘up’ or spin ‘down’. Our Spinny is in turn connected to a light bulb that glows when Spinny shows the output as 1 and doesn’t glow when the output is 0. Don’t be confused, yes I haven’t discussed how output works yet. If the spins of the particle are the same, the output is 1 while if the spins are different, the output is 0. In this scenario, the no. of macrostates is 2 as the output can be either 1 or 0. But, the no. of microstates will be 4. How? Let’s find out.
TABLE OF MICROSTATES
| Output | Spin | Bulb |
| 0 | Up & Down, Down & Up | Doesn’t glow |
| 1 | Up & Up,Down & Down | Glows |
Hopefully, this thing clears it up.
Wow, we learned a lot today. You might wanna take a break if you cannot continue at this moment. I can assure you that we are towards something more fundamental but you must bear with me. Many people have trouble getting the feel of Statistical Mechanics but I advise you to read till the end and experience the magic of the subject yourself.
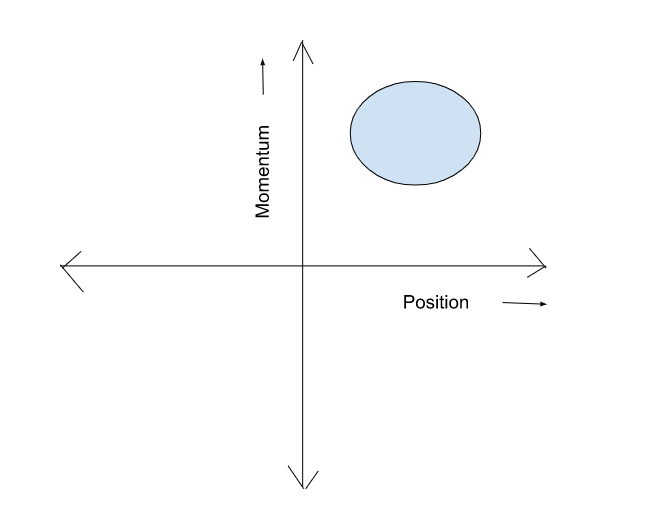
So, let’s continue! We now have a phase space(Ignore my drawing skills please), we have macrostates and microstates, and we have our ensemble. Let’s say we draw an arbitrary bound surface in the phase space. In the phase space, a point is defined by its position and momentum, the points defined within a phase space is called phase point. We need another definition to get to the next level, the phase points defined within a hypervolume give us the density. A density of states function(which is a function of position, momentum, and time) is defined to give us the no. of phase points within the hypervolume. As all the members of the ensemble continue to gradually change their microstates with time, the density function tells us how the ensemble is distributed over possible microstates at different instants of time. And this is where we shift our focus and move toward the fundamental postulates of statistical mechanics.
THE FUNDAMENTAL POSTULATES OF STATISTICAL MECHANICS
Usually, I am not a fan of the complicated. I am a man who prefers simple things or describing something using simple language. However, it is perhaps a necessity to describe a few things with the help of the complex. This is because what I am trying to define is actually something very fundamental to our subject. If I wanted to do it the simple way, I could just write the definition and with the common intuition of the human mind, the fundamental postulates will sound very normal to you, as if this has already been taken granted for and hence, you won’t get the essence of how actually important it is for our physical world. So, without further ado…
Let’s find our Spinny again and let’s do an experiment! Suppose we have 200 particles and we don’t know what their spin is. Our aim is to emit those 200 particles two at a time so our spinny can measure the output and then we have to count how many times the bulb glows. Therefore, we need to repeat the experiment a hundred times and then we get out the result. In technical terms, we are basically keeping the data of the macrostates(Bulb glows, Bulb doesn’t glow). We see that 50% of the time, the bulb glows while 50% of the time, it doesn’t glow. This is called the time average. The problem is that this kind of experiment is very time-consuming.
Now, we perform another experiment which is almost the same as the previous one. 200 particles in the box and we need to calculate how many times the bulb glows out of 100 times. However, here we have an ensemble of Spinny’s! Similarly, we need 100 bulbs where each Spinny is passing the data to its respective bulb. Even in this scenario, we find out that the probability of the bulb glowing is 50% and the bulb not glowing is also 50%. Let that sink in, you going to all the places in the world is equivalent to your mental copies existing in all the places of this world at this current instant of time. If this were not true, statistical mechanics does not work. The output depends only on the microstates(I shall clarify later) and hence the probability does not change and it gets more precise as no. of particles tends to infinity. Thus, we have our first postulate.
i) The ensemble average is equal to the time average. This is called the ergodic hypothesis.
Let’s repeat our first experiment which helped us grasp the concept of microstates. Now, we just change the rules a bit. The bulb glows only when the output is 1(as we all know) but the output is 1 only when we have two spin ‘up’s. Let’s visualize with a table here.
TABLE OF MICROSTATES
| Output | Spin | Bulb |
| 0 | Up Down, Down Up, Down Down | Does not glow |
| 1 | Up Up | Glows |
As we can see from the table, output 0 has three microstates while output 1 has 1 microstate. Therefore, if we repeat the experiment to find the ensemble average(or time average), we will find the probabilities to be different. The bulb glows 25% of the time while it doesn’t glow 75% of the time. How? This occurs due to the fact that 3 out of 4 microstates point towards the macrostate when the bulb does not glow and hence 75% probability and the same reason applies when the bulb glows. From here we get our second postulate.
ii) All the microstates of the system have equal probabilities. This is called equal a-priori probability hypothesis
You guys must be bored with the experiment thing so we are not gonna repeat or perform any experiment. Instead, we are gonna coin the term ‘equilibrium’. Basically, when we take two systems with energies E1 and E2, they interact and the energy flows from one system to another until they have the same energy. We now say that the energy of the two systems is in equilibrium or in other words, the tendency of a system is to move towards the equilibrium. However, in general cases, energy does not remain constant in a system, so we replace the energy with something called Temperature. An ensemble that has the properties of Temperature, Volume, and No. of particles constant is called a canonical ensemble. Now if we get more realistic, even if the no. of particles does not remain constant in a system, we then replace it with the chemical potential. The ensemble which has the properties of Temperature, Volume, and Chemical Potential as constant is called a grand canonical ensemble. I am not going to define the terms temperature and chemical potential as it is not in the scope of what I wanna discuss and we have already taken a detour to fill in the necessary gaps.
Now, getting back to the point, we can see that the output of the previous experiment was 0 for 75% of the time. Hence the system tends to occur more in this state. Rather, we can say that the system has the tendency to occur in the macrostate which has the most no. of corresponding microstates. As we can see from the previous paragraph, this thing is quite familiar to what we know about equilibrium. Therefore, the equilibrium state of a system is the one that has the most corresponding microstates. Our third postulate is,
iii) The tendency of a system is to attain its equilibrium state.
A TRANSITION FROM MICRO TO MACRO
From the information available now, we can modify our definition of the density of states function a bit. From the intuition, we developed so far(hopefully I was able to do that), we can say that the hypersurface resembles the macrostate of the system while the phase points are the microstates of that respective macrostate. We can then say that the no. of microstates(represented by a phase point in phase space) corresponding to the respective macrostate is called the density of states. The density function can be denoted as g(E) and it can be integrated over the phase space to find the number of states. But that’s something you can study yourself if you are interested in the mathematics. Since mathematics has already joined our discussion let me clarify a few things.
First of all, I am in no way an expert on the subject, I just try to spread the magic of science throughout the world. There is a probable chance that I am somewhat wrong in a few things but I can justify that by my actions of popularizing science. Yes, there are things that are not at all perfect in terms of definition as I cleverly mask the truth but here my mask is a medium that maps the definition of the scientific world to a world where the definitions are made much simpler so that everyone can understand it. In simple words yet again, to popularize science throughout the masses, we must lie to some extent(not my quote and I can’t seem to remember whose quote it was). Second of all, these topics can never be explained fully without the help of mathematics which I have avoided intentionally. Hence, you might find the last part to be bland as some things are beyond our physical intuition and I like to keep my lies as close to the truth as possible.
From the density of states, we can write an expression Z where,
Z = i g(Ei)exp(Ei/kT)dE
where Z is called the partition function(k is the Boltzmann constant).
There is no way that I can explain the partition function in simple words using physical intuition. However, if you know about the wavefunction, I can say that the partition function is just the statistical mechanics analog of it. In Quantum Mechanics, you can find out all the information of the state using the wavefunction. In Statistical Mechanics, the partition function does basically the same thing. You can find all about the macroscopic properties using the partition function. You can find the energy, entropy, pressure, and everything there is to know about the system. And personally, I find this insane! The fact that you can find everything there is to know, using a single function, isn’t it simply beautiful?
CONCLUSION
Just as I told you, the last part was pretty bland for my taste. Could not be satisfied with my writing. Hopefully, there will come a day in the future when people are not afraid of mathematics so the world could progress towards a better future. A future where no one is afraid to say what they want, where you do not have to think about how everyone will oppose you, and where you do not have to make compromises with your passion. It’s not that I am opposing the role of an audience, every artist needs an audience to motivate themselves. I am just saying that there are a lot of restrictions to every form of art and all I want is to see a world where everyone has an open mind. Anyways, let’s not move away from the topic.
There is a lot of research going on in Statistical Mechanics. For example, our Universe is not at all ergodic. This non-ergodicity of the Universe is quite an interesting research field. Similarly, ergodicity is broken in the case of long-range interacting systems. These kinds of interactions also result in a number of peculiar characteristics like negative specific heat, inequivalence of microcanonical and canonical ensembles, etc. There is also something called Non-Equilibrium Statistical Mechanics, research is also going on in the field of cosmological phase transitions. All in all, there is much to explore out there and to be brutally honest, I don’t know much about these myself. However, since I have already started dwelling on these fields, sooner or later I am gonna explore more into this field. This article has been long overdue and it is finally time that people start noticing this subject. And finally, I want to say that I have tried my best to present to my readers how magnificent statistical mechanics is. Hopefully, we shall meet again soon. Thank You.
REFERENCES
These are the books that helped me write this article
Fundamentals of Statistical Mechanics by F. Reif
Statistical Mechanics by R.K. Pathria
Statistical Mechanics by Kerson Huang
Intermediate Statistical Mechanics by Jayanta K. Bhattacharya and Dhruba Banerjee







Cheers!